【第三種電気主任技術者試験】電磁誘導の完全解説 - 発電・変圧の基礎理論
1. イントロダクション
私たちが日常生活で当たり前のように使っている電気。その電気を効率的に生み出し、変換し、利用するための基盤となる物理法則が「電磁誘導」です。スマートフォンの充電器、家庭用のコンセント、都市を明るく照らす電灯、そして工場の機械を動かす動力源など、現代の文明は電磁誘導の原理なしには成り立ちません。

電磁誘導とは、磁場の変化によって電気(起電力)が生じる現象です。この一見シンプルな原理が、現代の電力システム全体を支える基盤となっています。発電所で発電された電気は、変圧器によって電圧を変換されながら送電線を通じて私たちの家庭や職場へと届けられます。これらはすべて電磁誘導の原理に基づいています。
第三種電気主任技術者試験における重要性
電磁誘導は、第三種電気主任技術者試験の「理論」科目において最も重要な分野の一つです。特に「電気理論」分野では、電磁誘導の基本法則(ファラデーの法則、レンツの法則)から、発電機や変圧器の動作原理、交流回路の基礎まで、広範囲にわたって出題されます。この分野の理解が不十分だと、理論科目全体の得点に大きく影響するため、確実に理解しておく必要があります。例年の試験では、電磁誘導に関する基本的な計算問題や概念問題が複数出題されています。
本学習ページでは、電磁誘導の基本概念からその数学的表現、さらには実際の応用例まで段階的に解説していきます。電磁誘導の物理的な意味を理解し、実際の計算ができるようになることを目指します。また、第三種電気主任技術者試験でよく出題される問題パターンを取り上げ、実践的な演習も行います。
電磁誘導の理解は、電気工学の基礎を築く上で非常に重要です。この概念をマスターすることで、電気設備や機器の原理が明確になり、実務においても理論的な裏付けをもって判断できるようになります。一緒に学んでいきましょう。
2. 電磁誘導の基礎概念
2.1 ファラデーの発見と歴史的背景
電磁誘導の現象は、1831年にイギリスの科学者マイケル・ファラデー(Michael Faraday)によって発見されました。ファラデーは、磁石をコイルに近づけたり遠ざけたりすると、コイルに電流が流れることを見出しました。この発見は、それまで別々の現象と考えられていた電気と磁気の間に深い関連があることを示す画期的なものでした。
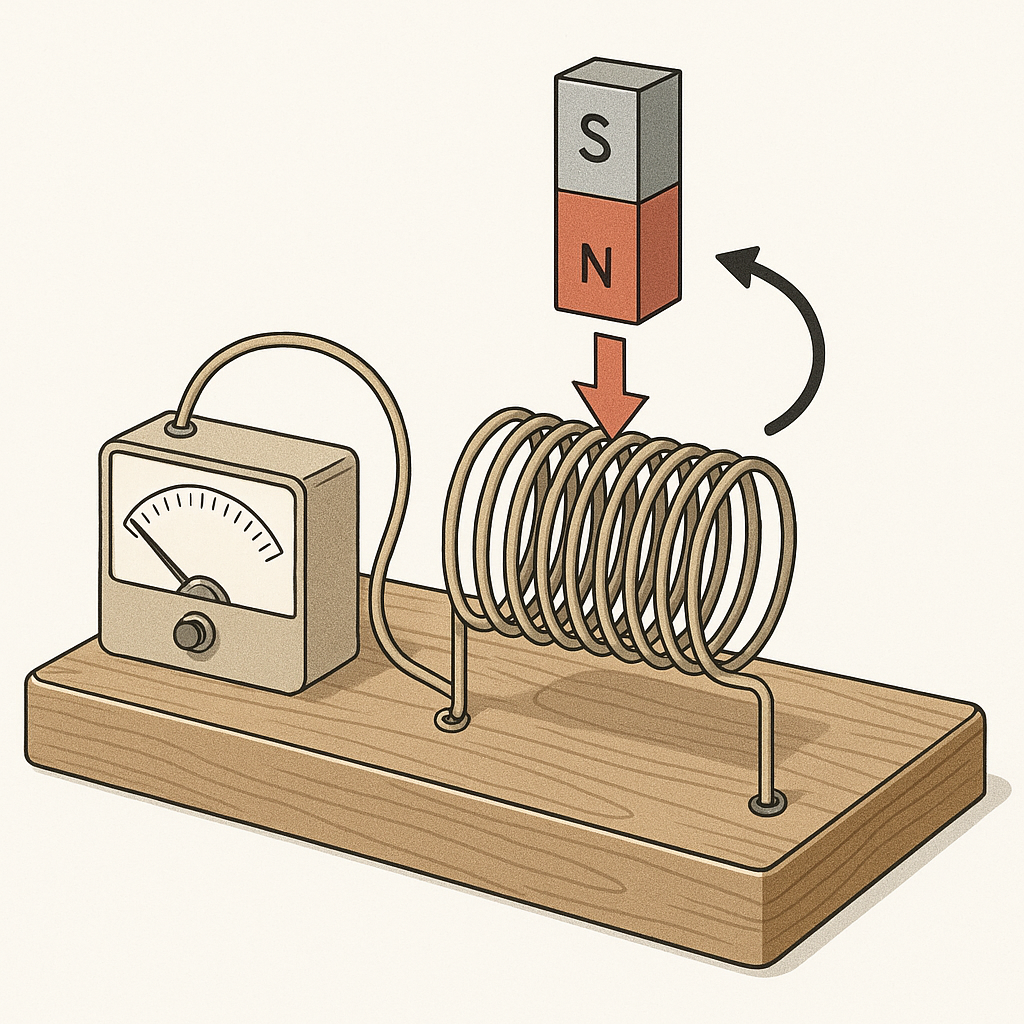
ファラデーは、コイルと磁石の相対的な動きが重要であり、「磁束の変化」が電流を生じさせると結論づけました。この発見は後に「ファラデーの法則」として定式化され、電気工学の基礎理論となりました。
ファラデーの実験
ファラデーは、鉄の輪に2つのコイルを巻き、一方のコイルにバッテリーを接続し、スイッチのON/OFFを繰り返しました。すると、もう一方のコイルに接続された検流計が、スイッチを入れた瞬間と切った瞬間だけ振れを示しました。これは、電流の「変化」によって生じる磁場の「変化」が、隣接するコイルに電流を誘導することを示しています。固定したコイルと磁石の間では、何も変化がない限り電流は生じないことも確認されました。
2.2 ファラデーの法則
ファラデーの法則は、電磁誘導の基本法則であり、次のように述べられます:
閉じた導体ループ(閉回路)に誘導される起電力は、そのループを貫く磁束の時間変化率に比例する。
数式で表すと:
ここで:
- \(\mathcal{E}\):誘導起電力 [V](ボルト)
- \(\Phi_B\):磁束 [Wb](ウェーバ)
- \(\frac{d\Phi_B}{dt}\):磁束の時間変化率 [Wb/s]
- 負号(マイナス)は、レンツの法則を表す(後述)
この法則は、磁束の変化が起電力を生じさせることを示しています。磁束が変化する原因としては、以下のようなものがあります:
- 磁場の強さ(磁束密度)の変化
- 導体ループの面積の変化
- 磁場と導体ループの相対的な角度の変化
- 導体が磁場内を移動する(導体の運動)
日常生活の例
自転車のダイナモ発電機は、電磁誘導の良い例です。車輪の回転によって、磁石が巻線の近くで回転します。この相対的な動きにより、巻線を貫く磁束が変化し、電流が発生します。この電流が自転車のライトを点灯させるのです。
2.3 レンツの法則
レンツの法則は、電磁誘導によって生じる電流の向きを規定するもので、次のように述べられます:
電磁誘導によって生じる電流は、その電流がつくる磁場が、電流を誘導した磁束の変化を打ち消す方向に流れる。
つまり、誘導電流は常に「原因となる磁束変化に抵抗する方向」に流れます。これは自然界におけるエネルギー保存の原理の現れでもあります。
レンツの法則を理解するための鍵は、「抵抗」あるいは「反作用」の概念です。例えば:
- 磁石をコイルに近づける(磁束増加)と、コイルは磁石を押し返すような磁場を作り出す電流を生じます
- 磁石をコイルから遠ざける(磁束減少)と、コイルは磁石を引き寄せるような磁場を作り出す電流を生じます
右ねじの法則による判断
右手の親指を磁場の方向に向け、残りの4本の指を閉じると、その指の向きが電流の向きを示します(右ねじの法則)。例えば、上向きの磁場が増加しているとき、それに抵抗するためには下向きの磁場が必要です。右ねじの法則によれば、これは時計回りの電流によって生じます。
なお、ファラデーの法則の式中にあるマイナス記号(負号)は、このレンツの法則を数学的に表現したものです。
2.4 磁束と磁束密度
電磁誘導を理解するためには、「磁束」と「磁束密度」の概念が重要です。
磁束密度(B)は、単位面積あたりの磁力線の数を表し、単位はテスラ(T)です。ベクトル量であり、方向と大きさを持ちます。
磁束(\(\Phi_B\))は、ある面積を貫く磁力線の総数を表し、単位はウェーバ(Wb)です。磁束密度と面積の積で求められるスカラー量です。
ここで:
- \(\Phi_B\):磁束 [Wb]
- \(\vec{B}\):磁束密度ベクトル [T]
- \(d\vec{A}\):微小面積ベクトル [m²](面に垂直な方向)
磁束密度が一様で、面が平面であり、磁束密度ベクトルと面の法線ベクトルがなす角度が \(\theta\) の場合、磁束は簡単な式で表せます:
ここで:
- \(B\):磁束密度の大きさ [T]
- \(A\):面積 [m²]
- \(\theta\):磁束密度ベクトルと面の法線ベクトルがなす角度
例題:磁束の計算
断面積 0.01 m² のコイルが、0.5 T の一様な磁場内に置かれている。コイルの法線ベクトルと磁場のなす角度が 30° のとき、コイルを貫く磁束を求めよ。
解答:
\begin{align*} \Phi_B &= BA\cos\theta \\ &= 0.5 \times 0.01 \times \cos 30° \\ &= 0.5 \times 0.01 \times 0.866 \\ &= 0.00433 \, \mathrm{Wb} = 4.33 \, \mathrm{mWb} \end{align*}電磁誘導の基礎概念まとめ
- 電磁誘導は、磁束の変化によって起電力が生じる現象
- ファラデーの法則:誘導起電力は磁束の時間変化率に比例(\(\mathcal{E} = -\frac{d\Phi_B}{dt}\))
- レンツの法則:誘導電流は、その原因となる磁束変化を打ち消す向きに流れる
- 磁束密度(B):単位面積あたりの磁力線の数 [T](テスラ)
- 磁束(\(\Phi_B\)):面を貫く磁力線の総数 [Wb](ウェーバ)
- 一様な磁場中の平面に対する磁束:\(\Phi_B = BA\cos\theta\)
3. 電磁誘導の数学的表現

3.1 ファラデーの法則の積分形
ファラデーの法則の積分形は、閉じた経路(閉回路)に沿った電界の線積分が、その経路が囲む面を通過する磁束の時間変化率に等しいことを示します:
ここで:
- \(\oint \vec{E} \cdot d\vec{l}\):閉経路に沿った電界の線積分(誘導起電力)[V]
- \(\frac{d}{dt}\int \vec{B} \cdot d\vec{A}\):経路が囲む面を通過する磁束の時間変化率 [Wb/s]
この式は、磁束の変化によって生じる「非保存的な電界」(渦電界)を表現しています。静電場の電界とは異なり、この電界では閉経路に沿った線積分がゼロにならず、起電力として現れます。
静電場と誘導電界の違い
静電場では \(\oint \vec{E} \cdot d\vec{l} = 0\) が成り立ちますが、時間変化する磁場がある場合は \(\oint \vec{E} \cdot d\vec{l} = -\frac{d\Phi_B}{dt} \neq 0\) となります。これは、誘導電界が「非保存場」であることを示しています。
3.2 ファラデーの法則の微分形
ファラデーの法則の微分形は、マクスウェル方程式の一部として表現され、空間の各点における電界と磁場の関係を示します:
ここで:
- \(\nabla \times \vec{E}\):電界のカール(回転)
- \(\frac{\partial \vec{B}}{\partial t}\):磁束密度の時間変化率
この式は、時間変化する磁場が「回転する電界」(渦電界)を生じさせることを示しています。この渦電界は、導体内に誘導電流を流す原因となります。
マクスウェル方程式における位置づけ
ファラデーの法則の微分形は、マクスウェルの4つの方程式の一つであり、電磁気学の基礎を成す重要な式です。これは、変化する磁場が電界を生み出すことを表現しており、電磁波の伝播や電磁誘導現象の根本的な理論となっています。
3.3 誘導起電力の計算方法
誘導起電力の計算には、磁束の時間変化を考慮する必要があります。磁束の変化は次のような要因で生じます:
- 磁束密度(B)の変化
- コイルの面積(A)の変化
- 磁場とコイル面の角度(\(\theta\))の変化
これらの要因を考慮した誘導起電力の一般式は:
これを展開すると:
\[\mathcal{E} = -\left[ A\cos\theta \frac{dB}{dt} + B\cos\theta \frac{dA}{dt} + BA(-\sin\theta) \frac{d\theta}{dt} \right]\]または、より簡潔に:
\[\mathcal{E} = -\left[ A\cos\theta \frac{dB}{dt} + B\cos\theta \frac{dA}{dt} + BA\sin\theta \frac{d\theta}{dt} \right]\]各項は、それぞれ次の要因による起電力を表しています:
- 第1項:磁束密度の変化による起電力
- 第2項:コイル面積の変化による起電力
- 第3項:磁場とコイル面の角度変化による起電力
コイルが N 巻きある場合、誘導起電力は N 倍になります:
例題:変化する磁場中のコイルの誘導起電力
面積 0.02 m² の 100 巻きコイルが、磁束密度が 0.1 T から 0.5 T まで 0.1 秒で直線的に増加する一様な磁場内に置かれている。コイルの面は磁場に垂直である。このとき、コイルに誘導される起電力を求めよ。
解答:
磁束の変化率を計算します:
誘導起電力は:
\begin{align*} \mathcal{E} &= -N\frac{d\Phi_B}{dt} \\ &= -100 \times 0.08 \\ &= -8 \, \mathrm{V} \end{align*}負号は、レンツの法則により、誘導電流が磁場の増加に抵抗する方向に流れることを示しています。起電力の大きさは 8 V です。
3.4 運動起電力
運動起電力(Motional EMF)は、導体が磁場内を移動するときに生じる起電力です。この現象は、ローレンツ力によって説明できます。
長さ L の導体が、磁束密度 B の一様な磁場内を速度 v で移動するとき、導体内の自由電子はローレンツ力 \(F = qvB\) を受けます。これにより導体の両端に電位差(起電力)が生じます:
ここで:
- \(\mathcal{E}\):運動起電力 [V]
- \(B\):磁束密度 [T]
- \(l\):導体の有効長さ [m]
- \(v\):導体の速度 [m/s]
導体、磁場、運動方向が互いに垂直の場合、最大の起電力が生じます。一般には、ベクトル積を用いて:
\[\mathcal{E} = (\vec{v} \times \vec{B}) \cdot \vec{l}\]例題:運動起電力の計算
長さ 30 cm の導体棒が、0.4 T の一様な磁場内を、磁場に垂直な方向に 5 m/s の速度で移動している。導体棒の両端に生じる起電力を求めよ。
解答:
\begin{align*} \mathcal{E} &= Blv \\ &= 0.4 \times 0.3 \times 5 \\ &= 0.6 \, \mathrm{V} \end{align*}したがって、導体棒の両端に生じる起電力は 0.6 V です。
電磁誘導の数学的表現まとめ
- ファラデーの法則の積分形:\(\oint \vec{E} \cdot d\vec{l} = -\frac{d\Phi_B}{dt}\)
- ファラデーの法則の微分形:\(\nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t}\)
- N 巻きコイルの誘導起電力:\(\mathcal{E} = -N\frac{d\Phi_B}{dt}\)
- 磁束の時間変化は、磁束密度 B の変化、面積 A の変化、角度 θ の変化のいずれかに起因する
- 運動起電力:\(\mathcal{E} = Blv\)(導体が磁場内を運動する場合)
- 誘導電流の向きは、レンツの法則によって決まる
4. 電磁誘導の応用
4.1 発電機の原理
発電機(ジェネレーター)は、電磁誘導の原理を利用して機械的エネルギーを電気エネルギーに変換する装置です。基本的な発電機は、磁場内でコイルを回転させることで誘導起電力を生成します。

発電機の主要部品:
- 固定子(ステーター):固定された部分。永久磁石または電磁石からなる磁場源
- 回転子(ローター):回転する部分。多数の導線で構成されたコイル
- スリップリング:回転子と外部回路を接続する装置(交流発電機の場合)
- 整流子:交流を直流に変換する装置(直流発電機の場合)
発電の原理:
- タービンなどの動力源により回転子が回転する
- コイルと磁場の間の相対運動により、コイルを貫く磁束が変化する
- 磁束の変化によって、コイルに誘導起電力が生じる
- 閉回路が形成されている場合、電流が流れる
交流発電機と直流発電機の違い
交流発電機(オルタネーター)は、磁場内で回転するコイルから直接交流電力を取り出します。一方、直流発電機(ダイナモ)は、整流子という機械的な仕組みを使って、コイルで発生した交流を直流に変換します。現代の電力系統では、主に交流発電機が使用され、必要に応じて交流から直流への変換が行われます。
正弦波交流発電の基本式
角速度 ω で回転する面積 A のコイル(N 巻き)が、磁束密度 B の一様な磁場内にあるとき、誘導される起電力は次式で表されます:
これは、周波数 f = ω/2π、最大値(振幅)E₀ = NBA ω の正弦波交流です。
\[\mathcal{E} = E_0\sin\omega t\]4.2 変圧器の原理
変圧器(トランスフォーマー)は、電磁誘導を利用して交流電圧を別の電圧レベルに変換する静止型の電気機器です。変圧器は、現代の電力システムで電力を効率的に送電し、各種電気機器に適した電圧を供給するために不可欠な存在です。


変圧器の主要部品:
- 鉄心:磁束を効率よく伝える強磁性体(通常はケイ素鋼板)
- 一次巻線:入力側の巻線(N₁巻き)
- 二次巻線:出力側の巻線(N₂巻き)
変圧器の動作原理:
- 一次巻線に交流電圧を印加すると、交流電流が流れる
- 一次巻線の電流により、鉄心内に時間変化する磁束が発生する
- この磁束は二次巻線も貫き、電磁誘導により二次巻線に起電力を誘導する
- 二次巻線に負荷が接続されていれば、二次回路に電流が流れる
理想変圧器の基本式:
\[\frac{V_1}{V_2} = \frac{N_1}{N_2}\]ここで:
- \(V_1\):一次側電圧 [V]
- \(V_2\):二次側電圧 [V]
- \(N_1\):一次巻線の巻数
- \(N_2\):二次巻線の巻数
また、パワーバランスから:
\[V_1 I_1 = V_2 I_2\]よって:
\[\frac{I_1}{I_2} = \frac{N_2}{N_1}\]ここで、\(I_1\)と\(I_2\)はそれぞれ一次電流と二次電流です。
変圧器と直流
変圧器は交流にのみ機能し、直流では機能しません。これは、磁束の「変化」が必要であり、直流の場合は磁束が一定となるため、二次側に起電力が誘導されないためです。
例題:変圧器の計算
一次巻線が500巻き、二次巻線が100巻きの変圧器がある。一次側に200 Vの交流電圧を印加したとき、二次側の電圧と、二次側で2 Aの電流が流れる場合の一次側の電流を求めよ。理想変圧器とする。
解答:
二次側電圧:
一次側電流:
\begin{align*} \frac{I_1}{I_2} &= \frac{N_2}{N_1} \\ \frac{I_1}{2} &= \frac{100}{500} \\ \frac{I_1}{2} &= \frac{1}{5} \\ I_1 &= \frac{2}{5} = 0.4 \, \mathrm{A} \end{align*}したがって、二次側電圧は40 V、一次側電流は0.4 Aです。
4.3 誘導電動機
誘導電動機(インダクションモーター)は、電磁誘導の原理を利用して電気エネルギーを機械的エネルギーに変換する装置です。特に三相誘導電動機は、その単純な構造と高い信頼性から、産業界で最も広く使用されている電動機の一つです。

誘導電動機の主要部品:
- 固定子(ステーター):三相巻線が配置された鉄心部分
- 回転子(ローター):「かご形」または「巻線形」の導体構造を持つ部分
誘導電動機の動作原理:
- 固定子巻線に三相交流を供給すると、回転磁界が発生する
- この回転磁界が回転子の導体を横切り、電磁誘導によって回転子に渦電流が発生する
- 渦電流と回転磁界の相互作用により、回転子にトルク(回転力)が発生する
- 回転子は磁界を追いかけるように回転するが、完全に追いつくことはない(すべり)
同期速度とすべり
回転磁界の回転速度(同期速度)\(n_s\)は、次式で表されます:
ここで、\(f\) は電源周波数 [Hz]、\(p\) は極対数です。例えば、4極機(p=4)で50 Hzの電源を使用する場合、同期速度は1500 rpmとなります。
誘導電動機の回転子速度 \(n\) は常に同期速度より低く、その差を「すべり」と呼びます:
\[s = \frac{n_s - n}{n_s}\]すべりは通常、定格負荷時に2〜5%程度です。
例題:誘導電動機の回転速度
6極の三相誘導電動機が60 Hzの電源で運転されている。すべりが4%のとき、回転子の回転速度を求めよ。
解答:
まず、同期速度を計算します:
次に、すべりから回転子速度を求めます:
\begin{align*} s &= \frac{n_s - n}{n_s} \\ 0.04 &= \frac{1200 - n}{1200} \\ 0.04 \times 1200 &= 1200 - n \\ 48 &= 1200 - n \\ n &= 1200 - 48 \\ &= 1152 \, \mathrm{rpm} \end{align*}したがって、回転子の回転速度は1152 rpmです。
4.4 渦電流とその応用
渦電流(うずでんりゅう、Eddy Currents)は、時間変化する磁場にさらされた導体内に誘導される環状の電流です。この現象は電磁誘導の一種で、様々な応用と対策が必要な問題の両面を持っています。
渦電流の特性:
- 導体内部を環状に流れる
- レンツの法則に従い、その原因となる磁束変化を打ち消す方向に流れる
- 導体内でジュール熱(I²R損失)を発生させる
- 磁束変化に抵抗する力(制動力)を生み出す
渦電流の応用:
- 誘導加熱:金属の熱処理、調理器具(IHクッキングヒーター)
- 電磁制動:電車のブレーキシステム、回転機器の制動
- 金属探知機:空港セキュリティ、産業用金属検出器
- 非破壊検査:金属部品の欠陥検出
- 電気計器:誘導形電力量計(積算電力計)
渦電流損失の低減方法
変圧器や電動機の鉄心では、渦電流による損失(渦電流損失)を低減するために、以下の対策が取られます:
- 積層構造(薄い鋼板の積層):渦電流の流れる経路を制限
- 高抵抗材料の使用:ケイ素鋼板など、電気抵抗の高い材料を使用
- 鋼板間の絶縁:鋼板表面に絶縁コーティングを施す
渦電流ブレーキの原理
電車の電磁ブレーキでは、レールに対して電磁石を近づけます。電磁石が作る磁場によってレール内に渦電流が発生し、その渦電流による磁場が元の磁場と相互作用して制動力を生みます。この制動力は車輪とレールの間の摩擦に依存しないため、雨や雪の日でも安定したブレーキ性能を発揮できます。また、機械的な摩耗が少ないという利点もあります。
電磁誘導の応用まとめ
- 発電機:機械的エネルギーを電気エネルギーに変換(磁場中でコイルを回転)
- 変圧器:電磁誘導を利用して交流電圧を変換(\(\frac{V_1}{V_2} = \frac{N_1}{N_2}\))
- 誘導電動機:回転磁界と電磁誘導により回転力を発生
- 渦電流:時間変化する磁場中の導体に誘導される環状電流
- 渦電流の応用:誘導加熱、電磁ブレーキ、金属探知機など
- 渦電流損失の低減:積層構造、高抵抗材料、絶縁処理
5. 実務における電磁誘導
5.1 電力発生システム
現代の電力供給システムは、電磁誘導の原理に基づく発電から始まります。発電所では様々な一次エネルギー源(火力、水力、原子力、風力など)を利用して発電機を回転させ、電力を生成しています。
主な発電方式:
- 火力発電:化石燃料(石炭、石油、天然ガス)の燃焼熱で水を沸騰させ、蒸気タービンを回転
- 水力発電:水の位置エネルギーを利用して水車を回転
- 原子力発電:核分裂の熱で水を沸騰させ、蒸気タービンを回転
- 風力発電:風の運動エネルギーで風車(ブレード)を回転
- 太陽光発電:光電効果を利用(直接電磁誘導を使用しない例外的な発電方式)
同期発電機
大規模発電所で主に使用される同期発電機は、回転子に直流電流を供給して電磁石を作り、それを回転させることで、固定子巻線に交流電圧を誘導します。回転子は常に一定速度(同期速度)で回転し、これにより一定周波数(日本では東日本50 Hz、西日本60 Hz)の交流電力が生成されます。
発電容量の計算例
発電機の出力は、次式で概算できます:
ここで、\(V\) は線間電圧 [V]、\(I\) は相電流 [A]、\(\cos\phi\) は力率です。例えば、線間電圧 6.6 kV、相電流 1000 A、力率 0.8 の三相同期発電機の出力は:
\begin{align*} P &= 6600 \times 1000 \times 0.8 \times \sqrt{3} \\ &= 6600 \times 1000 \times 0.8 \times 1.732 \\ &= 9.14 \times 10^6 \, \mathrm{W} \\ &= 9.14 \, \mathrm{MW} \end{align*}5.2 変圧器の設計と効率
変圧器は電力システムにおいて、発電、送電、配電、利用の各段階で電圧レベルを変換する重要な役割を担っています。変圧器の設計では、効率、絶縁、冷却、コストなど様々な要素を考慮する必要があります。
変圧器の損失と効率:
変圧器には主に2種類の損失があります:
- 鉄損(無負荷損):磁性体内での損失
- ヒステリシス損失:磁化の履歴による損失
- 渦電流損失:鉄心内に誘導される渦電流による損失
- 銅損(負荷損):巻線の抵抗による損失(I²R損失)
変圧器の効率は次式で計算できます:
ここで、\(P_{\text{out}}\) は出力電力、\(P_{\text{in}}\) は入力電力、\(P_{\text{loss}}\) は損失(鉄損+銅損)です。
変圧器の冷却方式
大型変圧器では発熱が問題となるため、効果的な冷却が必要です。主な冷却方式には以下があります:
- 乾式変圧器:空気で自然冷却または強制冷却
- 油入変圧器:絶縁油を冷媒として使用
- 自冷式:油の自然対流で冷却
- 風冷式:外部からファンで冷却
- 水冷式:冷却器内に水を循環
変圧器の効率計算
定格出力 100 kVA の変圧器が、鉄損 500 W、銅損 1200 W(定格負荷時)を持つ。力率 0.8 で定格の 80% の負荷で運転しているとき、変圧器の効率を求めよ。
解答:
出力電力:
銅損は負荷電流の二乗に比例するため:
\begin{align*} \text{銅損} &= 1200 \times (0.8)^2 \\ &= 1200 \times 0.64 \\ &= 768 \, \mathrm{W} = 0.768 \, \mathrm{kW} \end{align*}鉄損は負荷に関係なく一定なので、500 W = 0.5 kW
変圧器の効率:
\begin{align*} \eta &= \frac{P_{\text{out}}}{P_{\text{out}} + \text{鉄損} + \text{銅損}} \times 100 \\ &= \frac{64}{64 + 0.5 + 0.768} \times 100 \\ &= \frac{64}{65.268} \times 100 \\ &= 98.06 \, \% \end{align*}したがって、変圧器の効率は約 98.1% です。
5.3 誘導加熱
誘導加熱(Induction Heating)は、電磁誘導によって導体内に渦電流を発生させ、その導体自体を発熱させる技術です。高周波の交流電流を流したコイルの中に導体を置くと、導体内に渦電流が生じ、導体の電気抵抗によってジュール熱が発生します。
誘導加熱の主な特徴:
- 導体自体が発熱体となり、非接触で加熱できる
- 加熱速度が非常に速い(高効率)
- 表皮効果により、導体の表面から加熱される(表面硬化処理に有利)
- 加熱対象物のみを選択的に加熱できる
- 温度制御が容易で再現性が高い
誘導加熱の主な応用分野:
- 産業用:金属部品の熱処理(焼入れ、焼き戻し、焼きなまし)、溶接、溶融、鍛造
- 家庭用:IHクッキングヒーター、電磁調理器
- 医療用:ハイパーサーミア(癌治療)、歯科用機器
表皮効果(スキン効果)
高周波電流は導体の表面近くを流れる傾向があり、これを表皮効果と呼びます。表皮深さ δ(電流密度が表面値の1/e ≈ 37%になる深さ)は次式で表されます:
ここで、ρは導体の抵抗率、ωは角周波数(= 2πf)、μは導体の透磁率です。周波数が高いほど表皮深さは小さくなります。例えば、鉄では50 Hzで約3 mm、10 kHzでは約0.2 mmとなります。
IHクッキングヒーターの原理
IHクッキングヒーターでは、20~40 kHz程度の高周波電流をコイルに流します。鍋やフライパンなどの強磁性体の調理器具をコイル上に置くと、表皮効果により調理器具の底面に集中して渦電流が流れ、急速に加熱されます。アルミニウムや銅製の調理器具は電気抵抗が低いため発熱量が少なく、また、ガラスや陶器などの非導電性材料は渦電流が発生しないため加熱されません。このように、磁性体の鍋底のみを選択的に加熱できる点が特徴です。
5.4 電磁誘導による干渉と対策
電磁誘導は有用な応用がある一方で、望ましくない干渉(EMI: Electromagnetic Interference)を引き起こすこともあります。特に、電力線や高周波機器からの漏洩磁場が近くの電子機器や通信システムに誘導干渉を起こす問題は、電気主任技術者が理解しておくべき重要な課題です。
電磁誘導による干渉の主な例:
- 電力線からの誘導ノイズが通信回線に混入
- インバータやスイッチング電源からの高周波ノイズ
- モーターや変圧器からの漏れ磁場による影響
- 雷サージによる瞬間的な誘導電圧
- 無線周波数(RF)機器からの干渉
電磁干渉への主な対策:
- シールド(遮蔽):金属製の筐体やケーブルシールドで磁場や電場を遮断
- ツイストペア:導線をより合わせることで、誘導される電圧を相殺
- フィルタリング:ノイズ周波数を選択的に除去するフィルタ回路の使用
- グラウンディング:適切な接地で誘導電流の経路を提供
- 物理的分離:干渉源と感受性機器の間に十分な距離を確保
- フェライトコア:ケーブルに取り付けて高周波ノイズを吸収
EMC(電磁両立性)
EMC(Electromagnetic Compatibility)とは、電子機器が周囲の電磁環境に悪影響を与えずに正常に機能し、かつ周囲の電磁妨害に対して十分な耐性を持つことを指します。日本では電気用品安全法や電波法などで、機器のEMC特性に関する規制があります。電気主任技術者は、こうした規制や国際標準(IECなど)を理解し、設備の設計・保守においてEMC対策を適切に実施する必要があります。
ツイストペアケーブルの効果
平行な2本の導線が磁場 B の中にあると、その間に誘導電圧が生じます。しかし、導線をツイスト(より合わせ)することで、隣接するループで逆向きの誘導電圧が発生し、互いに打ち消し合います。例えば、単位長さあたり n 回ツイストされた場合、誘導ノイズは約 1/n に低減されます。これは、通信ケーブル(LANケーブルなど)で広く使用されている技術です。
実務における電磁誘導のまとめ
- 電力発生システムでは、様々な一次エネルギー源を利用して発電機を回転させ、電磁誘導により電力を生成
- 変圧器の効率は非常に高い(通常98%以上)が、大型変圧器では損失による発熱を冷却する必要がある
- 誘導加熱は、高周波電流による渦電流を利用して非接触で導体を加熱する技術
- 表皮効果により、高周波では電流が導体表面に集中し、表皮深さは周波数の平方根に反比例
- 望ましくない電磁誘導による干渉(EMI)を防ぐため、シールド、ツイストペア、フィルタリングなどの対策が必要
- EMC(電磁両立性)を確保するための規制や国際標準に従った設計・施工が重要
6. 演習問題
6.1 基本計算問題
問題1:磁束と誘導起電力
断面積 \(A = 0.005 \, \mathrm{m^2}\) の200巻きのコイルが、一様な磁場内に置かれている。磁束密度が \(B = 0.4 \, \mathrm{T}\) から \(B = 0.6 \, \mathrm{T}\) まで0.1秒間で直線的に増加するとき、コイルに誘導される起電力を求めよ。ただし、磁場はコイルの軸方向に平行とする。
解答:
ファラデーの法則により、誘導起電力は磁束の時間変化率に比例します:
\[\mathcal{E} = -N\frac{d\Phi_B}{dt}\]磁束の変化量を計算します:
\[\Delta\Phi_B = \Delta(BA) = A\Delta B = 0.005 \times (0.6 - 0.4) = 0.005 \times 0.2 = 0.001 \, \mathrm{Wb}\]磁束の時間変化率は:
\[\frac{d\Phi_B}{dt} = \frac{\Delta\Phi_B}{\Delta t} = \frac{0.001}{0.1} = 0.01 \, \mathrm{Wb/s}\]したがって、誘導起電力は:
\[\mathcal{E} = -N\frac{d\Phi_B}{dt} = -200 \times 0.01 = -2 \, \mathrm{V}\]負の符号は、レンツの法則により、誘導電流が磁場の増加に逆らう向きであることを示しています。誘導起電力の大きさは2 Vです。
問題2:運動誘導起電力
長さ \(l = 0.25 \, \mathrm{m}\) の導体棒が、磁束密度 \(B = 0.8 \, \mathrm{T}\) の一様な磁場内を、磁場に垂直な方向に \(v = 4 \, \mathrm{m/s}\) の速さで移動している。導体棒の両端に生じる起電力を求めよ。
解答:
運動誘導起電力の式を用います:
\[\mathcal{E} = Blv\]ここで、\(B\) は磁束密度、\(l\) は導体の長さ、\(v\) は速度です。これらの値を代入します:
\[\mathcal{E} = 0.8 \times 0.25 \times 4 = 0.8 \, \mathrm{V}\]したがって、導体棒の両端に生じる起電力は0.8 Vです。
問題3:変圧器の計算
一次巻線が1000巻き、二次巻線が250巻きの変圧器がある。一次側に240 Vの交流電圧を印加したとき、二次側の電圧と、二次側で4 Aの電流が流れる場合の一次側の電流を求めよ。理想変圧器として計算せよ。
解答:
理想変圧器における電圧比と巻数比の関係を用います:
\[\frac{V_1}{V_2} = \frac{N_1}{N_2}\]ここで、\(V_1 = 240 \, \mathrm{V}\)、\(N_1 = 1000\)、\(N_2 = 250\) です。二次側電圧 \(V_2\) を求めます:
\[\frac{240}{V_2} = \frac{1000}{250}\] \[V_2 = 240 \times \frac{250}{1000} = 240 \times 0.25 = 60 \, \mathrm{V}\]次に、理想変圧器の電流比と巻数比の関係を用います:
\[\frac{I_1}{I_2} = \frac{N_2}{N_1}\]ここで、\(I_2 = 4 \, \mathrm{A}\)、\(N_1 = 1000\)、\(N_2 = 250\) です。一次側電流 \(I_1\) を求めます:
\[\frac{I_1}{4} = \frac{250}{1000}\] \[I_1 = 4 \times \frac{250}{1000} = 4 \times 0.25 = 1 \, \mathrm{A}\]したがって、二次側電圧は60 V、一次側電流は1 Aです。
(確認:一次側電力 = 240 V × 1 A = 240 W、二次側電力 = 60 V × 4 A = 240 W で、電力保存則が成り立っています。)
6.2 過去問題
第三種電気主任技術者試験 過去問(類似問題)
断面積 \(A = 4 \times 10^{-4} \, \mathrm{m^2}\) の円形コイル(500巻き)がある。このコイルを、一様な磁束密度 \(B = 0.2 \, \mathrm{T}\) の磁場中に置き、磁場に対してコイルの軸が垂直になるように保持する。次に、コイルを180°回転させて、元の位置から磁場に対して軸が反対向きになるようにした。この回転を0.1秒間で行ったとき、コイルに誘導される平均起電力を求めよ。
解答:
初期状態と最終状態でのコイルを貫く磁束を計算します。
初期状態(コイルの軸が磁場に垂直、つまりコイルの面が磁場と平行):
\[\Phi_{\text{初期}} = BA\cos 90° = BA \times 0 = 0\]途中の状態(コイルの面が磁場に垂直):
\[\Phi_{\text{途中}} = BA\cos 0° = BA \times 1 = B \times A\]最終状態(コイルの軸が磁場に垂直だが反対向き):
\[\Phi_{\text{最終}} = BA\cos 90° = BA \times 0 = 0\]初期状態から90°回転した状態(コイルの面が磁場に垂直の状態)では、最大の磁束 \(BA\) がコイルを貫きますが、180°回転後の最終状態では再び磁束が0になります。つまり、0からBAまで増加し、再び0に戻る変化をしています。
しかし、誘導起電力を計算するには、コイルを貫く磁束の正味の変化を考える必要があります。初期状態と最終状態を比較すると、見かけ上は磁束の変化がないように見えますが、実際には磁束の向きが反転しています。つまり、180°回転することで磁束は \(0 \to +BA \to 0 \to -BA \to 0\) という変化をしており、正味の変化は \(2BA\) となります。
したがって、磁束の正味の変化量は:
\[|\Delta\Phi_B| = 2BA = 2 \times 0.2 \times 4 \times 10^{-4} = 1.6 \times 10^{-4} \, \mathrm{Wb}\]平均起電力の大きさは:
\[|\mathcal{E}_{\text{平均}}| = N\frac{|\Delta\Phi_B|}{\Delta t} = 500 \times \frac{1.6 \times 10^{-4}}{0.1} = 500 \times 1.6 \times 10^{-3} = 0.8 \, \mathrm{V}\]したがって、コイルに誘導される平均起電力の大きさは0.8 Vです。
第三種電気主任技術者試験 過去問(類似問題)
誘導起電力に関する以下の問いに答えよ。
(1) 直径 \(d = 10 \, \mathrm{cm}\) の円形コイル(20巻き)の中心軸が、地磁気の水平成分 \(B_H = 3 \times 10^{-5} \, \mathrm{T}\) に垂直になるように設置されている。このコイルを180°回転させて、中心軸の向きを反転したとき、コイルに誘導される起電力の平均値を求めよ。ただし、回転に要する時間は0.2秒とする。
(2) 上記のコイルの直径が2倍(\(d = 20 \, \mathrm{cm}\))の場合、同じ条件で同様の回転をさせたときの平均誘導起電力はいくらか。
解答:
(1) 直径 \(d = 10 \, \mathrm{cm}\) のコイル
円形コイルの面積を計算します:
\[A = \pi\left(\frac{d}{2}\right)^2 = \pi\left(\frac{0.1}{2}\right)^2 = \pi \times 0.0025 = 0.00785 \, \mathrm{m^2}\]問題4と同様に考えると、180°回転させることで磁束の正味の変化量は \(2BA\) となります:
\[|\Delta\Phi_B| = 2BA = 2 \times 3 \times 10^{-5} \times 0.00785 = 4.71 \times 10^{-7} \, \mathrm{Wb}\]平均起電力の大きさは:
\[|\mathcal{E}_{\text{平均}}| = N\frac{|\Delta\Phi_B|}{\Delta t} = 20 \times \frac{4.71 \times 10^{-7}}{0.2} = 20 \times 2.355 \times 10^{-6} = 4.71 \times 10^{-5} \, \mathrm{V}\]したがって、平均誘導起電力は約 \(4.71 \times 10^{-5} \, \mathrm{V}\) または \(47.1 \, \mu\mathrm{V}\) です。
(2) 直径 \(d = 20 \, \mathrm{cm}\) のコイル
直径が2倍になると、面積は4倍になります:
\[A' = \pi\left(\frac{d'}{2}\right)^2 = \pi\left(\frac{0.2}{2}\right)^2 = \pi \times 0.01 = 0.0314 \, \mathrm{m^2} = 4A\]誘導起電力は磁束の変化率に比例し、磁束は面積に比例するため、誘導起電力も4倍になります:
\[|\mathcal{E}'_{\text{平均}}| = 4 \times |\mathcal{E}_{\text{平均}}| = 4 \times 4.71 \times 10^{-5} = 1.884 \times 10^{-4} \, \mathrm{V}\]したがって、直径が2倍のコイルでの平均誘導起電力は約 \(1.88 \times 10^{-4} \, \mathrm{V}\) または \(188 \, \mu\mathrm{V}\) です。
演習問題のポイント
- 誘導起電力の計算では、磁束の時間変化率を正確に求めることが重要
- コイルの回転問題では、初期状態と最終状態の磁束の違いを考慮する
- 運動起電力の問題では、磁場、導体の長さ、速度の関係を正しく理解する
- 変圧器の問題では、巻数比と電圧比・電流比の関係を使いこなす
- 実際の試験では計算ミスを防ぐため、単位の取り扱いに注意すること
- レンツの法則による向きの判断にも気を配ること
7. まとめ
本ページでは、第三種電気主任技術者試験の重要分野である「電磁誘導」について学習しました。電磁誘導の基本原理から応用までを体系的に解説し、実際の計算方法や試験対策のポイントを紹介しました。
重要ポイントの要約
• 電磁誘導とは、磁束の変化によって起電力が生じる現象である
• ファラデーの法則:誘導起電力は磁束の時間変化率に比例(\(\mathcal{E} = -N\frac{d\Phi_B}{dt}\))
• レンツの法則:誘導電流は、その原因となる磁束変化を打ち消す向きに流れる
• 磁束 \(\Phi_B = BA\cos\theta\):磁束密度、面積、角度に依存
• 運動起電力:導体が磁場を横切る際に生じる起電力(\(\mathcal{E} = Blv\))
• 変圧器の原理:電磁誘導を利用して交流電圧を変換(\(\frac{V_1}{V_2} = \frac{N_1}{N_2}\))
• 渦電流:導体内に誘導される環状電流(誘導加熱や電磁ブレーキに応用)
電磁誘導の理解は、電気主任技術者として必須の知識です。この原理は発電機や変圧器などの電力機器の基本動作を支え、現代の電力システム全体の根幹をなしています。また、電磁誘導は産業界や日常生活でも広く応用されており、技術者として実務に携わる上でも重要な概念です。
第三種電気主任技術者試験では、電磁誘導に関する基本的な理解と計算能力が問われます。本ページで学んだ概念や計算方法をマスターすることで、試験での得点力向上につながるでしょう。特に、誘導起電力の計算、変圧器の原理、渦電流の性質などは頻出テーマですので、しっかりと理解しておきましょう。
次の学習では、「交流回路」について学びます。電磁誘導の理解が、交流発電や交流回路の動作原理を理解する基礎となります。一つ一つの概念を確実に理解しながら、電気理論の全体像を構築していきましょう。